Note: The following article contains spoilers about the Netflix series “3 Body Problem.”
I first encountered the three-body problem 60 years ago, in a short story called “Placet is a Crazy Place” by American science fiction writer Frederic Brown.
In Brown’s story, Placet is a planet in a figure-of-eight orbit around two stars, one of which is composed of ordinary matter, the other of anti-matter. The closeness of the two stars cause time and space to become wonderfully distorted so that Placet can eclipse itself. But, intriguingly, the orbit is assumed to be stable and predictable.
Chinese science fiction writer Liu Cixin’s epic trilogy, Rememberance of Earth’s Past, returns to imagining what could happen when three celestial bodies are in orbit around each other. The first instalment, The Three-Body Problem, has been adapted into a series by Netflix.
The opening scenes of 3 Body Problem, set in Beijing in the early days of the Cultural Revolution, are particularly powerful. The characters in the series are flawed — the scientists are highly intelligent, but their ambitions, failings and fears are all too clear.
Random motion
The plot of 3 Body Problem involves an alien race, known as the Trisolarians, inhabiting a planet orbiting a nearby star system, known as Alpha Centauri. This consists of three stars that follow continuously changing orbits, causing the planet to go from bitter cold to searing heat in a matter of minutes.
The motion of the stars is unpredictable, so the Trisolarians cannot anticipate the arrival of the so-called chaotic eras that lead to the planet-wide destruction of their environment.
Intriguingly, Alpha Centauri actually is a triple-star system, consisting of two stars that orbit each other closely over a period of nearly 80 years, and a much more distant third star. This is very different from the system represented in 3 Body Problem.
So could we imagine a system where the stars are so close together in their orbits that their motion becomes random?

(ESA/NASA)
Possible orbits
The answer lies at the heart of theoretical physics. Isaac Newton famously solved the two-body problem for the Earth-moon system in the 1660s, so we can predict the moon’s orbit with extraordinary precision.
It is a little surprising that this works so well, because we are ignoring the sun which would turn it into a three-body problem. The trick to handling this (one of many) is that we can find a solution that works for the Earth-moon and then add in the effect of the sun, which turns out to be small.
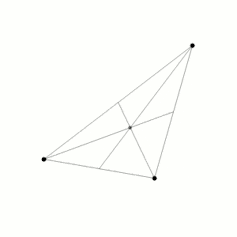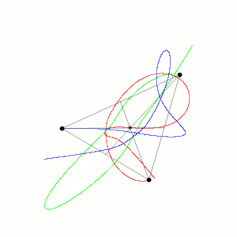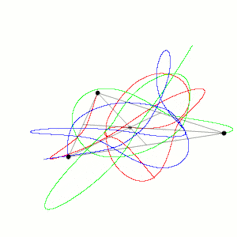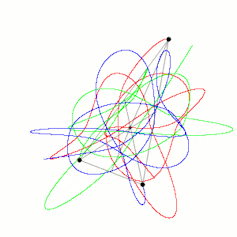
We have learned a great deal since Newton. There is no general solution for the three-body problem: we cannot write down a formula for how three bodies will move in general. We have found a whole host of special cases; even the figure-of-eight orbit of the fictional Placet is possible.
Also, the James Webb telescope has been ingeniously placed to provide another solution for the three-body problem. It orbits around the sun, beyond the moon’s orbit of the Earth, so it can be shielded from radiation as much as possible.
It is complicated but straightforward for a computer to find solutions for the three-body problem. Cosmologists have been using computational analysis to construct increasingly complex models of how the universe evolved from an almost totally uniform beginning to its present stage. These models typically run with more than 10 billion bodies.
Chaotic systems
So why should we be interested in something as mundane as three bodies? Because if we have a system of three objects, all massive and fairly close, their motion is chaotic. This means that even though we can find out almost exactly what happens to them over a short period of time, it becomes unpredictable over a long time. But note that I have not told you what long and short means in this context.
(Dnttllthmmnm/Wikimedia Commons), CC BY
We can get a feeling for this if we look at the weather, another chaotic system, and specifically hurricanes. We can accurately predict where a hurricane will make landfall 12 hours in advance — two days in advance we can make a rough prediction, but a week in advance is impossible.
As three bodies in orbit move, they dance across the sky in an extraordinarily complex fashion. We have no way of guessing where each of the bodies might be located in 1,000 years. They may not even be around: there are examples where one of the stars in a polyamorous threesome would be ejected totally, leaving behind a double-star system.
Unpredictable systems
In 3 Body Problem the challenge is that the orbits cause the climate to flip with essentially no warning. This is characteristic of a different kind of situation, a so-called stochastic problem.
A classic example is a drunk trying to navigate his way to the door, when every step is followed by another in a random direction. You cannot predict where the next step will take him, but you can say that he will eventually reach the door. It is a little bit scary that such systems are at the heart of our civilization, as demonstrated by the gyrations of the stock market. But stars — and the climate they produce — are not stochastic.
The fictional Alpha Centauri that the Trisolarians inhabit represents a chaotic system, predictable accurately in the short term but unpredictable over thousands of years. But it would be much simpler for them to predict it than to invade Earth. As with a lot of science fiction, enjoy it for the fiction and not the science.![]()
Peter Watson, Emeritus professor, Physics, Carleton University
This article is republished from The Conversation under a Creative Commons license. Read the original article.










